Пифагор Самосский

Пифагор Самосский — древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев.

Биография

Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров. Ещё Геродот называл его «величайшим эллинским мудрецом». Основными источниками по жизни и учению Пифагора являются сочинения философа-неоплатоника Ямвлиха (242—306 гг.) «О Пифагоровой жизни»; Порфирия (234—305 гг.) «Жизнь Пифагора»; Диогена Лаэртского (200—250 гг.) кн. 8, «Пифагор». Эти авторы опирались на сочинения более ранних авторов, из которых следует отметить ученика Аристотеля Аристоксена (370—300 гг. до н. э.) родом из Тарента, где сильны были позиции пифагорейцев. Таким образом, самые ранние известные источники об учении Пифагора появились лишь 200 лет спустя после его смерти. Сам Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей, не всегда беспристрастных.

Родителями Пифагора были Мнесарх и Партенида с острова Самос. Мнесарх был камнерезом (Диоген Лаэртский); по словам же Порфирия он был богатым купцом из Тира, получившим самосское гражданство за раздачу хлеба в неурожайный год. Первая версия предпочтительнее, так как Павсаний приводит генеалогию Пифагора по мужской линии от Гиппаса из пелопоннесского Флиунта, бежавшего на Самос и ставшего прадедом Пифагора. Партенида, позднее переименованная мужем в Пифаиду, происходила из знатного рода Анкея, основателя греческой колонии на Самосе.

Рождение ребёнка будто бы предсказала Пифия в Дельфах, потому Пифагор и получил своё имя, которое значит «тот, о ком объявила Пифия». В частности, Пифия сообщила Мнесарху, что Пифагор принесет столько пользы и добра людям, сколько не приносил и не принесет в будущем никто другой. Поэтому, на радостях, Мнесарх дал жене новое имя Пифаида и дал имя ребёнку Пифагор. Пифаида сопровождала мужа в его поездках, и Пифагор родился в Сидоне Финикийском (по Ямвлиху) примерно в 570 до н. э.

По словам античных авторов, Пифагор встретился чуть ли не со всеми известными мудрецами той эпохи, греками, персами, халдеями, египтянами, впитал в себя всё накопленное человечеством знание. В популярной литературе иногда приписывают Пифагору Олимпийскую победу в боксе, путая Пифагора-философа с его тёзкой (Пифагором, сыном Кратета с Самоса), который одержал свою победу на 48-х Играх за 18 лет до рождения знаменитого философа.

В юном возрасте Пифагор отправился в Египет, чтобы набраться мудрости и тайных знаний у египетских жрецов. Диоген и Порфирий пишут, что самосский тиран Поликрат снабдил Пифагора рекомендательным письмом к фараону Амасису, благодаря чему он был допущен к обучению и посвящён в таинства, запретные для прочих чужеземцев.

Ямвлих пишет, что Пифагор в 18-летнем возрасте покинул родной остров и, объехав мудрецов в разных краях света, добрался до Египта, где пробыл 22 года, пока его не увёл в Вавилон в числе пленников персидский царь Камбиз, завоевавший Египет в 525 до н. э. В Вавилоне Пифагор пробыл ещё 12 лет, общаясь с магами, пока наконец не смог вернуться на Самос в 56-летнем возрасте, где соотечественники признали его мудрым человеком.

По Порфирию, Пифагор покинул Самос из-за несогласия с тиранической властью Поликрата в 40-летнем возрасте. Так как эти сведения основываются на словах Аристоксена, источника IV века до н. э., то считаются относительно достоверными. Поликрат пришёл к власти в 535 до н. э., отсюда дата рождения Пифагора оценивается в 570 до н. э., если допустить, что он уехал в Италию в 530 до н. э. Ямвлих сообщает, что Пифагор переехал в Италию в 62-ю Олимпиаду, то есть в 532—529 гг. до н. э. Эти сведения хорошо согласуются с Порфирием, но полностью противоречат легенде самого Ямвлиха (вернее, одного из его источников) о вавилонском пленении Пифагора. Точно неизвестно, посещал ли Пифагор Египет, Вавилон или Финикию, где набрался по легендам восточной мудрости. Диоген Лаэртский цитирует Аристоксена, который говорил, что учение своё, по крайней мере что касается наставлений по образу жизни, Пифагор воспринял от жрицы Фемистоклеи Дельфийской, то есть в местах не столь отдалённых для греков.

Разногласия с тираном Поликратом вряд ли могли послужить причиной отъезда Пифагора, скорее ему требовалось возможность проповедовать свои идеи и, более того, претворять своё учение в жизнь, что затруднительно осуществить в Ионии и материковой Элладе, где жило много искушённых в вопросах философии и политики людей. Ямвлих сообщает:

«Его философия распространилась, вся Эллада стала восхищаться им, и лучшие и мудрейшие мужи приезжали к нему на Самос, желая слушать его учение. Сограждане, однако, принуждали его участвовать во всех посольствах и общественных делах. Пифагор чувствовал, как тяжело, подчиняясь законам отечества, одновременно заниматься философией, и видел, что все прежние философы прожили жизнь на чужбине. Обдумав всё это, отойдя от общественных дел и, как говорят некоторые, считая недостаточной невысокую оценку самосцами его учения, он уехал в Италию, считая своим отечеством страну, где больше способных к обучению людей.»

Пифагор поселился в греческой колонии Кротоне в Южной Италии, где нашёл много последователей. Их привлекала не только мистическая философия, которую он убедительно излагал, но и предписываемый им образ жизни с элементами здорового аскетизма и строгой морали. Пифагор проповедовал нравственное облагораживание невежественного народа, достигнуть которого возможно там, где власть принадлежит касте мудрых и знающих людей, и которым народ повинуется в чём-то безоговорочно, как дети родителям, а в остальном сознательно, подчиняясь нравственному авторитету. Ученики Пифагора образовали своего рода религиозный орден, или братство посвящённых, состоящий из касты отобранных единомышленников, буквально обожествляющих своего учителя — основателя ордена. Этот орден фактически пришёл в Кротоне к власти, однако из-за антипифагорейских настроений в конце VI в. до н. э. Пифагору пришлось удалиться в другую греческую колонию Метапонт, где он и умер. Почти 450 лет спустя во времена Цицерона (I в. до н. э.) в Метапонте как одну из достопримечательностей показывали склеп Пифагора.

У Пифагора была жена по имени Феано, сын Телавг и дочь Мня (по другой версии сын Аримнест и дочь Аригнота).

По Ямвлиху, Пифагор возглавлял своё тайное общество тридцать девять лет, тогда приблизительная дата смерти Пифагора может быть отнесена к 491 до н. э., к началу эпохи греко-персидских войн. Диоген, ссылаясь на Гераклида (IV в. до н. э.), говорит, что Пифагор мирно скончался в возрасте 80 лет, или же в 90 лет (по неназванным другим источникам). Из этого следует дата смерти 490 до н. э. (или 480 до н. э., что маловероятно). Евсевий Кесарийский в своей хронографии обозначил 497 до н. э. как год смерти Пифагора.

Разгром пифагорейского союза

Среди последователей и учеников Пифагора оказалось немало представителей знати, которые пытались изменить законы в своих городах в соответствии с пифагорейским учением. На это наложилась обычная борьба той эпохи между олигархической и демократической партиями в древнегреческом обществе. Недовольство большинства населения, не разделяющего идеалов философа, вылилось в кровавые мятежи в Кротоне и Таренте.

Ямвлих со ссылкой на Аполлония, который пользовался архивами из Кротона, излагает разгром пифагорейцев в Кротоне так:

«Пифагорейцы образовали большое сообщество (их было более трёхсот), но оно составляло лишь небольшую часть города, который уже не управлялся согласно тем же обычаям и нравам. Впрочем, пока кротонцы владели своей землёй, и Пифагор находился у них, сохранялось государственное устройство, существовавшее от основания города, хотя были недовольные, ожидавшие удобного случая для переворота. Но когда завоевали Сибарис, Пифагор уехал, а пифагорейцы, управлявшие завоёванной землёй, не распределили её по жребию, как хотело большинство, то затаённая ненависть вспыхнула, и множество граждан выступило против них… Родственники пифагорейцев относились с ещё большим раздражением к тому, что те подают правую руку только своим, а из близких — только родителям, и что они предоставляют своё имущество для общего пользования, а от имущества родственников оно отделено. Когда родственники начали эту вражду, остальные с готовностью присоединились к конфликту… Через много лет… кротонцами овладели сожаление и раскаяние, и они решили вернуть в город тех пифагорейцев, которые ещё были живы.»

Много пифагорейцев погибло, выжившие рассеялись по Италии и Греции. Немецкий историк Ф. Шлоссер замечает по поводу разгрома пифагорейцев: «Кончилась совершенной неудачей попытка перенести в Грецию кастовый и клерикальный быт и, наперекор духу народа, изменить его политическое устройство и нравы по требованиям отвлечённой теории.»

Согласно Порфирию и сам Пифагор погиб в результате антипифагорейского мятежа в Метапонте, однако другие авторы не подтверждают этой версии, хотя охотно передают историю о том, будто бы удручённый философ уморил себя голодом в священном храме.

Философское учение

Учение Пифагора следует разбить на две составляющие части: научный подход к познанию мира и религиозно-мистический образ жизни, проповедуемый Пифагором. Доподлинно неизвестны заслуги Пифагора в первой части, так как ему позднее приписывали всё, созданное последователями в рамках школы пифагореизма. Вторая часть превалирует в учении Пифагора, и именно она осталась в сознании большинства античных авторов.

В сохранившихся работах Аристотель никогда прямо не обращается непосредственно к Пифагору, но лишь к «так называемым пифагорейцам». В потерянных работах (известных по выдержкам) Аристотель рассматривает Пифагора как основателя полурелигиозного культа, который запрещал есть бобы и имел золотое бедро, но не принадлежал к последовательности мыслителей, предшественников Аристотеля.

Платон относился к Пифагору с глубочайшим почтением и уважением. Когда пифагореец Филолай впервые опубликовал 3 книги, излагающие основные положения пифагореизма, Платон по совету друзей немедленно их купил за большие деньги.

Деятельность Пифагора как религиозного новатора VI в. до н. э. заключалась в создании тайного общества, которое не только ставило перед собой политические цели (из-за чего пифагорейцев разгромили в Кротоне), но, главным образом, освобождение души путём нравственного и физического очищения с помощью тайного учения (мистическое учение о круговороте переселений души). По Пифагору, вечная душа переселяется с небес в бренное тело человека или животного и претерпевает ряд переселений, пока не заслужит права вернуться обратно на небеса.

В акусматах (изречениях) Пифагора содержатся обрядовые наставления: о круговороте человеческих жизней, поведении, жертвоприношениях, погребениях, питании. Акусматы сформулированы лаконично и доступно для понимания любого человека, в них содержатся также постулаты общечеловеческой морали. Более сложная философия, в рамках которой развивалась математика и другие науки, предназначалась для «посвящённых», то есть избранных людей, достойных владеть тайным знанием. Научная составляющая учения Пифагора развивалась в V в. до н. э. усилиями его последователей (Архит из Тарента, Филолай из Кротона, Гиппас из Метапонта), но сошла на нет в IV в. до н. э., в то время как мистическо-религиозная составляющая получила своё развитие и второе рождение в виде неопифагореизма во времена Римской империи.

Заслугой пифагорейцев было выдвижение мысли о количественных закономерностях развития мира, что содействовало развитию математических, физических, астрономических и географических знаний. В основе вещей лежит число, учил Пифагор, познать мир — значит познать управляющие им числа. Изучая числа, пифагорейцы разработали числовые отношения и нашли их во всех областях человеческой деятельности. Числа и пропорции изучались с тем, чтобы познать и описать душу человека, а познав, управлять процессом переселения душ с конечной целью отправить душу в некое высшее божественное состояние.

Как отмечал И. Д. Рожанский: «Несмотря на пережитки магического мышления, основная идея Пифагора о том, что в основе всех вещей лежат числа или отношения чисел, оказалась очень плодотворной». Как отмечал Стобей: «Судя по всему, больше всех (наук) Пифагор почитал науку о числах, он продвинул её вперёд, выведя её за пределы употребления в торговле и выражая, моделируя все вещи числами» (1, «Проэмий», 6, с. 20).

Несмотря на встречающееся мнение о том, что Пифагор будто бы был вегетарианцем, Диоген Лаэрский пишет, что Пифагор изредка ел рыбу, воздерживался только от пахотных быков и от баранов, а остальных животных дозволял в пищу.

В качестве критика Пифагора выступал его современник Гераклит: «Пифагор, Мнесархов сын, занимался собиранием сведений больше всех людей на свете и, понадергав себе эти сочинения, выдал за свою собственную мудрость многознайство и мошенничество». По Диогену Лаэртскому, в продолжении известного изречения Гераклита «Многознание уму не научает» упоминается среди прочих и Пифагор: «а не то научило бы Гесиода и Пифагора, равно как и Ксенофана с Гекатеем».

Научные достижения

В современном мире Пифагор считается великим математиком и космологом древности, однако ранние свидетельства до III в. до н. э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев.»

Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Такое мнение основывается на сведениях Аполлодора-исчислителя (личность не идентифицирована) и на стихотворных строках (источник стихов не известен):

«В день, когда Пифагор открыл свой чертёж знаменитый,
Славную он за него жертву быками воздвиг.»

Современные историки предполагают, что Пифагор не доказывал теорему, но мог передать грекам это знание, известное в Вавилоне за 1000 лет до Пифагора (согласно вавилонским глиняным табличкам с записями математических уравнений). Хотя сомнение в авторстве Пифагора существует, но весомых аргументов, чтобы это оспорить, нет.

Аристотель затрагивает развитие представлений о космологии в работе «Метафизика», однако вклад Пифагора в ней никак не озвучен. По Аристотелю космологическими теориями занимались пифагорейцы в середине V в. до н. э., но, видимо, не сам Пифагор. Пифагору приписывают открытие, что Земля — шар, но то же открытие наиболее авторитетный автор в этом вопросе, Феофраст, отдаёт Пармениду. Да и Диоген Лаэртский сообщает, что суждение о шарообразности Земли высказывал Анаксимандр Милетский, у которого учился Пифагор в юности.

В то же время, научные заслуги школы пифагорейцев в математике и космологии бесспорны. Точку зрения Аристотеля, отражённую в его несохранившемся трактате «О пифагорейцах», передал Ямвлих. По Аристотелю, истинными пифагорейцами были акусматики, последователи религиозно-мистического учения о переселении душ. Акусматики рассматривали математику как учение, исходящее не столько от Пифагора, сколько от пифагорейца Гиппаса. В свою очередь математики-пифагорейцы, по их собственному мнению, вдохновлялись направляющим учением Пифагора для углублённого изучения своей науки.

Сочинения Пифагора

Пифагор не писал трактатов. Из устных наставлений для простого народа невозможно составить трактат, а тайное оккультное учение для избранных нельзя было доверить книге. Ямвлих так комментирует отсутствие трудов Пифагора:

«Замечательно также и их упорство в неразглашении учения: за столько лет до поколения Филолая, как представляется, никто не столкнулся ни с одним пифагорейским сочинением. Филолай первым из пифагорейцев опубликовал три нашумевшие книги, которые, как говорят, Дион из Сиракуз купил за сто мин по указанию Платона, когда Филолай впал в крайнюю нужду.»

Диоген перечисляет названия этих книг, приписываемых Пифагору: «О воспитании», «О государстве» и «О природе». Однако ни один из авторов в первые 200 лет после смерти Пифагора, включая Платона, Аристотеля и их преемников в Академии и Лицее, не приводит цитат из трудов Пифагора или хотя бы указывает на существование таких трудов. С начала новой эры античным писателям неизвестны труды Пифагора, как сообщили о том Плутарх, Иосиф Флавий и Гален.

В III в. до н. э. появилась компиляция высказываний Пифагора, известная под названием «Священное слово», из которой позднее возникли так называемые «Золотые стихи» (иногда их относят к IV в. до н. э. без веских оснований). Впервые цитаты из этих стихов цитируются Хрисиппом в III в. до н. э., хотя, возможно, в то время компиляция ещё не сложилась в законченный вид. Заключительный отрывок из «Золотых стихов» в переводе И. Петер:

Ты же будь твёрдым: божественный род присутствует в смертных,
Им, возвещая, священная всё открывает природа.
Если не чуждо это тебе, ты наказы исполнишь,
Душу свою исцелишь и от множества бедствий избавишь.
Яства, сказал я, оставь те, что я указал в очищеньях
И руководствуйся подлинным знанием — лучшим возничим.
Если ты, тело покинув, в свободный эфир вознесёшься,
Станешь нетленным, и вечным, и смерти не знающим богом.

Альберт Эйнштейн

Альберт Эйнштейн — физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 года, общественный деятель-гуманист. Жил в Германии (1879—1893, 1914—1933), Швейцарии (1893—1914) и США (1933—1955). Почётный доктор около 20 ведущих университетов мира, член многих Академий наук, в том числе иностранный почётный член АН СССР (1926).

Биография

Альберт Эйнштейн родился 14 марта 1879 года в южногерманском городе Ульме, в небогатой еврейской семье.

Герман Эйнштейн и Паулина Эйнштейн (урождённая Кох), отец и мать учёногоОтец, Герман Эйнштейн (1847—1902), был в это время совладельцем небольшого предприятия по производству перьевой набивки для матрацев и перин. Мать, Паулина Эйнштейн (урождённая Кох, 1858—1920), происходила из семьи состоятельного торговца кукурузой Юлиуса Дерцбахера (в 1842 году он сменил фамилию на Кох) и Йетты Бернхаймер. Летом 1880 года семья переселилась в Мюнхен, где Герман Эйнштейн вместе с братом Якобом основал небольшую фирму по торговле электрическим оборудованием. В Мюнхене родилась младшая сестра Альберта Мария (Майя, 1881—1951).Начальное образование Альберт Эйнштейн получил в местной католической школе. По его собственным воспоминаниям, он в детстве пережил состояние глубокой религиозности, которое оборвалось в 12 лет. Через чтение научно-популярных книг он пришёл к убеждению, что многое из того, что изложено в Библии, не может быть правдой, а государство намеренно занимается обманом молодого поколения. Всё это сделало его вольнодумцем и навсегда породило скептическое отношение к авторитетам. Из детских впечатлений Эйнштейн позже вспоминал как наиболее сильные: компас, «Начала» Евклида и (около 1889 года) «Критику чистого разума» Иммануила Канта. Кроме того, по инициативе матери он с шести лет начал заниматься игрой на скрипке. Увлечение музыкой сохранялось у Эйнштейна на протяжении всей жизни. Уже находясь в США в Принстоне, в 1934 году Альберт Эйнштейн дал благотворительный концерт, где исполнял на скрипке произведения Моцарта в пользу эмигрировавших из нацистской Германии учёных и деятелей культуры.

В гимназии он не был в числе первых учеников (исключение составляли математика и латынь). Укоренившаяся система механического заучивания материала учащимися (которая, как он позже говорил, наносит вред самому духу учёбы и творческому мышлению), а также авторитарное отношение учителей к ученикам вызывало у Альберта Эйнштейна неприятие, поэтому он часто вступал в споры со своими преподавателями.В 1894 году Эйнштейны переехали из Мюнхена в итальянский город Павию, близ Милана, куда братья Герман и Якоб перевели свою фирму. Сам Альберт оставался с родственниками в Мюнхене ещё некоторое время, чтобы окончить все шесть классов гимназии. Так и не получив аттестата зрелости, в 1895 году он присоединился к своей семье в Павии.

Осенью 1895 года Альберт Эйнштейн прибыл в Швейцарию, чтобы сдать вступительные экзамены в Высшее техническое училище (Политехникум) в Цюрихе и стать преподавателем физики. Блестяще проявив себя на экзамене по математике, он в то же время провалил экзамены по ботанике и французскому языку, что не позволило ему поступить в Цюрихский Политехникум. Однако директор училища посоветовал молодому человеку поступить в выпускной класс школы в Арау (Швейцария), чтобы получить аттестат и повторить поступление.В кантональной школе Арау Альберт Эйнштейн посвящал своё свободное время изучению электромагнитной теории Максвелла. В сентябре 1896 года он успешно сдал все выпускные экзамены в школе, за исключением экзамена по французскому языку, и получил аттестат, а в октябре 1896 года был принят в Политехникум на педагогический факультет. Здесь он подружился с однокурсником, математиком Марселем Гроссманом (1878—1936), а также познакомился с сербской студенткой факультета медицины Милевой Марич (на 4 года старше его), впоследствии ставшей его женой. В этом же году Эйнштейн отказался от германского гражданства. Чтобы получить швейцарское гражданство, требовалось уплатить 1000 швейцарских франков, однако бедственное материальное положение семьи позволило ему сделать это только спустя 5 лет. Предприятие отца в этом году окончательно разорилось, родители Эйнштейна переехали в Милан, где Герман Эйнштейн, уже без брата, открыл фирму по торговле электрооборудованием.Стиль и методика преподавания в Политехникуме существенно отличались от закостеневшей и авторитарной прусской школы, поэтому дальнейшее обучение давалось юноше легче. У него были первоклассные преподаватели, в том числе замечательный геометр Герман Минковский (его лекции Эйнштейн часто пропускал, о чём потом искренне сожалел) и аналитик Адольф Гурвиц.

Квантовая теория

Для разрешения проблемы, вошедшей в историю под названием «Ультрафиолетовой катастрофы», и соответствующего согласования теории с экспериментом Макс Планк предположил (1900), что излучение и поглощение света веществом происходит дискретно (неделимыми порциями), и энергия излучаемой порции зависит от частоты света. Некоторое время эту гипотезу даже сам её автор рассматривал как условный математический приём, однако Эйнштейн во второй из вышеупомянутых статей предложил далеко идущее её обобщение и с успехом применил для объяснения свойств фотоэффекта. Эйнштейн выдвинул тезис, что не только излучение, но и распространение и поглощение света дискретны; позднее эти порции (кванты) получили название фотонов. Этот тезис позволил ему объяснить две загадки фотоэффекта: почему фототок возникал не при всякой частоте света, а только начиная с определённого порога, зависящего только от вида металла, а энергия и скорость вылетающих электронов зависели не от интенсивности света, а только от его частоты. Теория фотоэффекта Эйнштейна с высокой точностью соответствовала опытным данным, что позднее подтвердили эксперименты Милликена (1916).

Первоначально эти взгляды встретили непонимание большинства физиков, даже Планка Эйнштейну пришлось убеждать в реальности квантов. Постепенно, однако, накопились опытные данные, убедившие скептиков в дискретности электромагнитной энергии. Последнюю точку в споре поставил эффект Комптона (1923).

В 1907 году Эйнштейн опубликовал квантовую теорию теплоёмкости (старая теория при низких температурах сильно расходилась с экспериментом). Позже (1912) Дебай, Борн и Карман уточнили теорию теплоёмкости Эйнштейна, и было достигнуто отличное согласие с опытом.

Броуновское движение

В 1827 году Роберт Броун наблюдал под микроскопом и впоследствии описал хаотическое движение цветочной пыльцы, плававшей в воде. Эйнштейн, на основе молекулярной теории, разработал статистико-математическую модель подобного движения. На основании его модели диффузии можно было, помимо прочего, с хорошей точностью оценить размер молекул и их количество в единице объёма. Одновременно к аналогичным выводам пришёл Смолуховский, чья статья была опубликована на несколько месяцев позже, чем Эйнштейна. Свои работы по статистической механике, под названием «Новое определение размеров молекул», Эйнштейн представил в Политехникум в качестве диссертации и в том же 1905 году получил звание доктора философии (эквивалент кандидата естественных наук) по физике. В следующем году Эйнштейн развил свою теорию в новой статье «К теории броуновского движения», и в дальнейшем неоднократно возвращался к этой теме.

Вскоре (1908) измерения Перрена полностью подтвердили адекватность модели Эйнштейна, что стало первым экспериментальным доказательством молекулярно-кинетической теории, подвергавшейся в те годы активным атакам со стороны позитивистов.

Макс Борн писал (1949): «Я думаю, что эти исследования Эйнштейна больше, чем все другие работы, убеждают физиков в реальности атомов и молекул, в справедливости теории теплоты и фундаментальной роли вероятности в законах природы». Работы Эйнштейна по статистической физике цитируются даже чаще, чем его работы по теории относительности[. Выведенная им формула для коэффициента диффузии и его связи с дисперсией координат оказалась применимой в самом общем классе задач: марковские процессы диффузии, электродинамика и т. п.

Позднее, в статье «К квантовой теории излучения» (1917) Эйнштейн, исходя из статистических соображений, впервые предположил существование нового вида излучения, происходящего под воздействием внешнего электромагнитного поля («индуцированное излучение»). В начале 1950-х годов был предложен способ усиления света и радиоволн, основанный на использовании индуцированного излучения, а в последующие годы оно легло в основу теории лазеров.

Общая теория относительности

Ещё Декарт объявил, что все процессы во Вселенной объясняются локальным взаимодействием одного вида материи с другим, и с точки зрения науки этот тезис близкодействия был естественным. Однако ньютоновская теория всемирного тяготения резко противоречила тезису близкодействия — в ней сила притяжения передавалась непонятно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. На протяжении двух веков делались попытки исправить положение и избавиться от мистического дальнодействия, наполнить теорию тяготения реальным физическим содержанием — тем более что после Максвелла гравитация осталась единственным в физике пристанищем дальнодействия. Особенно неудовлетворительной стала ситуация после утверждения специальной теории относительности, так как теория Ньютона не была лоренц-ковариантной. Однако до Эйнштейна исправить положение никому не удалось.

Искривление пространства массивным телом

Основная идея Эйнштейна была проста: материальным носителем тяготения является само пространство (точнее, пространство-время). Тот факт, что гравитацию можно рассматривать как проявление свойств геометрии четырёхмерного неевклидова пространства, без привлечения дополнительных понятий, есть следствие того, что все тела в поле тяготения получают одинаковое ускорение («принцип эквивалентности» Эйнштейна). Четырёхмерное пространство-время при таком подходе оказывается не «плоской и безразличной сценой» для материальных процессов, у него имеются физические атрибуты, и в первую очередь — метрика и кривизна, которые влияют на эти процессы и сами зависят от них. Если специальная теория относительности — это теория неискривлённого пространства, то общая теория относительности, по замыслу Эйнштейна, должна была рассмотреть более общий случай, пространство-время с переменной метрикой (псевдориманово многообразие). Причиной искривления пространства-времени является присутствие материи, и чем больше её энергия, тем искривление сильнее. Ньютоновская же теория тяготения представляет собой приближение новой теории, которое получается, если учитывать только «искривление времени», то есть изменение временно?й компоненты метрики, g_{00} (пространство в этом приближении евклидово). Распространение возмущений гравитации, то есть изменений метрики при движении тяготеющих масс, происходит с конечной скоростью. Дальнодействие с этого момента исчезает из физики.

Математическое оформление этих идей было достаточно трудоёмким и заняло несколько лет (1907—1915). Эйнштейну пришлось овладеть тензорным анализом и создать его четырёхмерное псевдориманово обобщение; в этом ему помогли консультации и совместная работа сначала с Марселем Гроссманом, ставшим соавтором первых статей Эйнштейна по тензорной теории гравитации, а затем и с «королём математиков» тех лет, Давидом Гильбертом. В 1915 г. главные уравнения общей теории относительности Эйнштейна (ОТО), обобщающие ньютоновские, были опубликованы почти одновременно в статьях Эйнштейна и Гильберта.

Новая теория тяготения предсказала два ранее неизвестных физических эффекта, вполне подтверждённые наблюдениями, а также точно и полностью объяснила вековое смещение перигелия Меркурия, долгое время приводившее в недоумение астрономов. После этого теория относительности стала практически общепризнанным фундаментом современной физики. Кроме астрофизики, ОТО нашла практическое применение, как уже упоминалось выше, в системах глобального позиционирования (Global Positioning Systems, GPS), где расчёты координат производятся с очень существенными релятивистскими поправками.

Исаак Ньютон

Исаак Ньютон — английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета и многие другие математические и физические теории.

Биография

Исаак Ньютон, сын мелкого, но зажиточного фермера Исаака Ньютона (1606—1642), родился в деревне Вулсторп (англ. Woolsthorpe, графство Линкольншир), в канун гражданской войны. Отец Ньютона не дожил до рождения сына. Мальчик родился преждевременно, был болезненным, поэтому его долго не решались крестить. И всё же он выжил, был крещён (1 января[K 2]), и назван Исааком в честь покойного отца. Факт рождения под Рождество Ньютон считал особым знаком судьбы[1]. Несмотря на слабое здоровье в младенчестве, он прожил 84 года.
Ньютон искренне считал, что его род восходит к шотландским дворянам XV века, однако историки обнаружили, что в 1524 году его предки были бедными крестьянами. К концу XVI века семья разбогатела и перешла в разряд йоменов (землевладельцев). Отец Ньютона оставил в наследство крупную по тем временам сумму в 500 фунтов стерлингов и несколько сот акров плодородной земли, занятой полями и лесами.
В январе 1646 года мать Ньютона, Анна Эйскоу (англ. Hannah Ayscough)[K 3] (1623—1679) вновь вышла замуж. От нового мужа, 63-летнего вдовца, у неё было трое детей, и она стала уделять мало внимания Исааку. Покровителем мальчика стал его дядя по матери, Уильям Эйскоу. В детстве Ньютон, по отзывам современников, был молчалив, замкнут и обособлен, любил читать и мастерить технические игрушки: солнечные и водяные часы, мельницу и т. п. Всю жизнь он чувствовал себя одиноким.
Отчим умер в 1653 году, часть его наследства перешла к матери Ньютона и была сразу же оформлена ею на Исаака. Мать вернулась домой, однако основное внимание уделяла троим младшим детям и обширному хозяйству; Исаак по-прежнему был предоставлен сам себе.
В 1655 году 12-летнего Ньютона отдали учиться в расположенную неподалёку школу в Грэнтеме, где он жил в доме аптекаря Кларка. Вскоре мальчик показал незаурядные способности, однако в 1659 году мать Анна вернула его в поместье и попыталась возложить на 16-летнего сына часть дел по управлению хозяйством. Попытка не имела успеха — Исаак предпочитал всем другим занятиям чтение книг, стихосложение и особенно конструирование различных механизмов. В это время к Анне обратился Стокс, школьный учитель Ньютона, и начал уговаривать её продолжить обучение необычайно одарённого сына; к этой просьбе присоединились дядя Уильям и грэнтемский знакомый Исаака (родственник аптекаря Кларка) Хэмфри Бабингтон, член Кембриджского Тринити-колледжа. Объединёнными усилиями они, в конце концов, добились своего. В 1661 году Ньютон успешно окончил школу и отправился продолжать образование в Кембриджский университет.

Философия и научный метод

Ньютон решительно отверг популярный в конце XVII века подход Декарта и его последователей-картезианцев, который предписывал при построении научной теории вначале «проницательностью ума» найти «первопричины» исследуемого явления. На практике этот подход часто приводил к выдвижению надуманных гипотез о «субстанциях» и «скрытых свойствах», не поддающихся опытной проверке. Ньютон считал, что в «натуральной философии» (то есть физике) допустимы только такие предположения («принципы», сейчас предпочитают название «законы природы»), которые прямо вытекают из надёжных экспериментов, обобщают их результаты; гипотезами же он называл предположения, недостаточно обоснованные опытами. «Всё…, что не выводится из явлений, должно называться гипотезою; гипотезам же метафизическим, физическим, механическим, скрытым свойствам не место в экспериментальной философии». Примерами принципов служат закон тяготения и 3 закона механики в «Началах»; слово «принципы» (Principia Mathematica, традиционно переводимое как «математические начала») содержится и в названии его главной книги.
В письме к Пардизу Ньютон сформулировал «золотое правило науки»:

Лучшим и наиболее безопасным методом философствования, как мне кажется, должно быть сначала прилежное исследование свойств вещей и установление этих свойств с помощью экспериментов, а затем постепенное продвижение к гипотезам, объясняющим эти свойства. Гипотезы могут быть полезны лишь при объяснении свойств вещей, но нет необходимости взваливать на них обязанности определять эти свойства вне пределов, выявленных экспериментом… ведь можно изобрести множество гипотез, объясняющих любые новые трудности.

Такой подход не только ставил вне науки умозрительные фантазии (например, рассуждения картезианцев о свойствах «тонких материй», будто бы объясняющих электромагнитные явления), но был более гибким и плодотворным, потому что допускал математическое моделирование явлений, для которых первопричины ещё не обнаружены. Это и произошло с тяготением и теорией света — их природа прояснилась гораздо позже, что не мешало успешному многовековому применению ньютоновских моделей.
Знаменитая фраза «гипотез не измышляю» (лат. Hypotheses non fingo), конечно, не означает, что Ньютон недооценивал важность нахождения «первопричин», если они однозначно подтверждаются на опыте. Полученные из эксперимента общие принципы и следствия из них должны также пройти опытную проверку, которая может привести к корректировке или даже смене принципов. «Вся трудность физики… состоит в том, чтобы по явлениям движения распознать силы природы, а затем по этим силам объяснить остальные явления».
Ньютон, так же как Галилей, полагал, что в основе всех процессов природы лежит механическое движение:

Было бы желательно вывести из начал механики и остальныеявления природы… ибо многое заставляет меня предполагать, что все эти явления обусловливаются некоторыми силами, с которыми частицы тел, вследствие причин покуда неизвестных, или стремятся друг к другу и сцепляются в правильные фигуры, или же взаимно отталкиваются и удаляются друг от друга. Так как эти силы неизвестны, то до сих пор попытки философов объяснить явления природы и оставались бесплодными.

Свой научный метод Ньютон сформулировал в книге «Оптика»:

Как в математике, так и при испытании природы, при исследовании трудных вопросов, аналитический метод должен предшествовать синтетическому. Этот анализ заключается в том, что из экспериментов и наблюдений посредством индукции выводят общие заключения и не допускают против них никаких возражений, которые не исходили бы из опытов или других надёжных истин. Ибо гипотезы не рассматриваются в экспериментальной философии. Хотя полученные посредством индукции из экспериментов и наблюдений результаты не могут ещё служить доказательством всеобщих заключений, всё же это — наилучший путь делать заключения, который допускает природа вещей.

В 3-ю книгу «Начал» (начиная со 2-го издания) Ньютон поместил ряд методических правил, направленных против картезианцев; первый из них — вариант «бритвы Оккама»:

Правило I. Не должно принимать в природе иных причин сверх тех, которые истинны и достаточны для объяснения явлений… природа ничего не делает напрасно, а было бы напрасным совершать многим то, что может быть сделано меньшим. Природа проста и не роскошествует излишними причинами вещей…
Правило IV. В опытной физике предложения, выведенные из совершающихся явлений с помощью наведения [индукции], несмотря на возможность противных им предположений, должны быть почитаемы за верные или в точности, или приближённо, пока не обнаружатся такие явления, которыми они ещё более уточняются или же окажутся подверженными исключениям.

Механистические взгляды Ньютона оказались неверны — не все явления природы вытекают из механического движения. Однако его научный метод утвердился в науке. Современная физика успешно исследует и применяет явления, природа которых ещё не выяснена (например, элементарные частицы. Начиная с Ньютона, естествознание развивается, твёрдо уверенное в том, что мир познаваем, потому что природа устроена по простым математическим принципам. Эта уверенность стала философской базой для грандиозного прогресса науки и технологии.

Математика

Первые математические открытия Ньютон сделал ещё в студенческие годы: классификация алгебраических кривых 3-го порядка (кривые 2-го порядка исследовал Ферма) ибиномиальное разложение произвольной (не обязательно целой) степени, с которого начинается ньютоновская теория бесконечных рядов — нового и мощнейшего инструмента анализа. Разложение в ряд Ньютон считал основным и общим методом анализа функций, и в этом деле достиг вершин мастерства. Он использовал ряды для вычисления таблиц, решения уравнений (в том числе дифференциальных), исследования поведения функций. Ньютон сумел получить разложение для всех стандартных на тот момент функций.
Ньютон разработал дифференциальное и интегральное исчисление одновременно с Г. Лейбницем (немного раньше) и независимо от него. До Ньютона действия с бесконечно малымине были увязаны в единую теорию и носили характер разрозненных остроумных приёмов (см. Метод неделимых). Создание системного математического анализа сводит решение соответствующих задач, в значительной степени, до технического уровня. Появился комплекс понятий, операций и символов, ставший отправной базой дальнейшего развития математики. Следующий, XVIII век, стал веком бурного и чрезвычайно успешного развития аналитических методов.
Возможно, Ньютон пришёл к идее анализа через разностные методы, которыми много и глубоко занимался. Правда, в своих «Началах» Ньютон почти не использовал бесконечно малых, придерживаясь античных (геометрических) приёмов доказательства, но в других трудах применял их свободно.
Отправной точкой для дифференциального и интегрального исчисления были работы Кавальери и особенно Ферма, который уже умел (для алгебраических кривых) проводитькасательные, находить экстремумы, точки перегиба и кривизну кривой, вычислять площадь её сегмента. Из других предшественников сам Ньютон называл Валлиса, Барроу и шотландского учёного Джеймса Грегори. Понятия функции ещё не было, все кривые он трактовал кинематически как траектории движущейся точки.
Уже будучи студентом, Ньютон понял, что дифференцирование и интегрирование — взаимно обратные операции. Эта основная теорема анализа уже более или менее ясно вырисовывалась в работах Торричелли, Грегори и Барроу, однако лишь Ньютон понял, что на этой основе можно получить не только отдельные открытия, но мощное системное исчисление, подобное алгебре, с чёткими правилами и гигантскими возможностями.
Ньютон почти 30 лет не заботился о публикации своего варианта анализа, хотя в письмах (в частности, к Лейбницу) охотно делится многим из достигнутого. Тем временем вариант Лейбница широко и открыто распространяется по Европе с 1676 года. Лишь в 1693 году появляется первое изложение варианта Ньютона — в виде приложения к «Трактату по алгебре»Валлиса. Приходится признать, что терминология и символика Ньютона по сравнению с лейбницевской довольно неуклюжи: флюксия (производная), флюэнта (первообразная), момент величины (дифференциал) и т. п. Сохранились в математике только ньютоновское обозначение «o» для бесконечно малой dt (впрочем, эту букву в том же смысле использовал ранее Грегори), да ещё точка над буквой как символ производной по времени.
Достаточно полное изложение принципов анализа Ньютон опубликовал только в работе «О квадратуре кривых» (1704), приложенной к его монографии «Оптика». Почти весь изложенный материал был готов ещё в 1670—1680-е годы, но лишь теперь Грегори и Галлей уговорили Ньютона издать работу, которая, с опозданием на 40 лет, стала первым печатным трудом Ньютона по анализу. Здесь у Ньютона появляются производные высших порядков, найдены значения интегралов разнообразных рациональных и иррациональных функций, приведены примеры решения дифференциальных уравнений 1-го порядка.

В 1707 году вышла книга «Универсальная арифметика». В ней приведены разнообразные численные методы. Ньютон всегда уделял большое внимание приближённому решению уравнений. Знаменитый метод Ньютона позволял находить корни уравнений с немыслимой ранее скоростью и точностью (опубликован в «Алгебре» Валлиса, 1685). Современный вид итерационному методу Ньютона придал Джозеф Рафсон (1690).
В 1711 году наконец был напечатан, спустя 40 лет, «Анализ с помощью уравнений с бесконечным числом членов». В этом труде Ньютон с одинаковой лёгкостью исследует как алгебраические, так и «механические» кривые (циклоиду, квадратрису). Появляются частные производные. В этом же году выходит «Метод разностей», где Ньютон предложил интерполяционную формулу для проведении через (n + 1) данные точки с равноотстоящими или неравноотстоящими абсциссами многочлена n-го порядка. Это разностный аналог формулы Тейлора.
В 1736 году был посмертно издан итоговый труд «Метод флюксий и бесконечных рядов», существенно продвинутый по сравнению с «Анализом с помощью уравнений». В нём приводятся многочисленные примеры отыскания экстремумов, касательных и нормалей, вычисления радиусов и центров кривизны в декартовых и полярных координатах, отыскания точек перегиба и т. п. В этом же сочинении произведены квадратуры и спрямления разнообразных кривых.
Надо отметить, что Ньютон не только достаточно полно разработал анализ, но и сделал попытку строго обосновать его принципы. Если Лейбниц склонялся к идее актуальных бесконечно малых, то Ньютон предложил (в «Началах») общую теорию предельных переходов, которую несколько витиевато назвал «метод первых и последних отношений». Используется именно современный термин «предел» (лат. limes), хотя внятное описание сущности этого термина отсутствует, подразумевая интуитивное понимание. Теория пределов изложена в 11 леммах книги I «Начал»; одна лемма есть также в книге II. Арифметика пределов отсутствует, нет доказательства единственности предела, не выявлена его связь с бесконечно малыми. Однако Ньютон справедливо указывает на большую строгость такого подхода по сравнению с «грубым» методом неделимых. Тем не менее в книге II, введя «моменты» (дифференциалы), Ньютон вновь запутывает дело, фактически рассматривая их как актуальные бесконечно малые
Примечательно, что теорией чисел Ньютон совершенно не интересовался. По всей видимости, физика ему была гораздо ближе математики.

Механика

Заслугой Ньютона является решение двух фундаментальных задач.

• Создание для механики аксиоматической основы, которая фактически перевела эту науку в разряд строгих математических теорий.
• Создание динамики, связывающей поведение тела с характеристиками внешних воздействий на него (сил).

Кроме того, Ньютон окончательно похоронил укоренившееся с античных времён представление, что законы движения земных и небесных тел совершенно различны. В его модели мира вся Вселенная подчинена единым законам, допускающим математическую формулировку.

Аксиоматика Ньютона состояла из трёх законов, которые сам он сформулировал в следующем виде.

1. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.2. Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.3. Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.

Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов этот принцип является прямым следствием уравнений динамики (следствие V в «Началах»). Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».

Ньютон также дал строгие определения таких физических понятий, как количество (не вполне ясно использованное у Декарта) и сила. Он ввёл в физику понятие массы как меры инерции и, одновременно, гравитационных свойств. Ранее физики пользовались понятием вес, однако вес тела зависит не только от самого тела, но и от его окружения (например, от расстояния до центра Земли), поэтому понадобилась новая, инвариантная характеристика.

Завершили математизацию механики Эйлер и Лагранж.

Всемирное тяготение

Аристотель и его сторонники считали тяжесть стремлением тел «подлунного мира» к их естественным местам. Некоторые другие античные философы (среди них Эмпедокл, Платон) полагали тяжесть стремлением родственных тел к соединению. В XVI веке эту точку зрения поддержал Николай Коперник, в гелиоцентрической системе которого Земля считалась лишь одной из планет. Близких взглядов придерживались Джордано Бруно, Галилео Галилей. Иоганн Кеплер считал, что причиной падения тел является не их внутренние стремления, но сила притяжения со стороны Земли, причем не только Земля притягивает камень, но и камень притягивает Землю. По его мнению, сила тяжести распространяется по меньшей мере до Луны. В своих поздних работах он высказывал мнение, что сила тяжести убывает с расстоянием и взаимному притяжению подвержены все тела Солнечной системы. Физическую природу тяжести пытались разгадать Рене Декарт, Жиль Роберваль, Христиан Гюйгенс и другие учёные XVII века.
Тот же Кеплер первым предположил, что движение планет управляется силами, исходящими от Солнца. В его теории было три таких силы: одна, круговая, подталкивает планету по орбите, действуя по касательной к траектории (за счёт этой силы планета и движется), другая то притягивает, то отталкивает планету от Солнца (за счёт неё орбита планеты является эллипсом) и третья действует поперек плоскости эклиптики (благодаря чему орбита планеты лежит в одной плоскости). Круговую силу он считал убывающей обратно пропорционально расстоянию от Солнца. Ни одна из этих трёх сил не отождествлялась с тяжестью. Кеплерову теорию отверг ведущий астроном-теоретик середины XVII века Исмаэль Буллиальд, по мнению которого, во-первых, планеты движутся вокруг Солнца не под действием исходящих от него сил, а в силу внутреннего стремления, а во-вторых, если бы круговая сила и существовала, она убывала бы обратно второй степени расстояния, а не первой, как считал Кеплер. Декарт полагал, что планеты переносятся вокруг Солнца гигантскими вихрями.
Предположение о существовании исходящей от Солнца силы, управляющей движением планет, высказывал Джереми Хоррокс. По мнению Джованни Альфонсо Борелли, от Солнца исходят три силы: одна продвигает планету по орбите, другая притягивает планету к Солнцу, третья (центробежная), наоборот, отталкивает планету. Эллиптическая орбита планеты является результатом противоборства двух последних. В 1666 г. Роберт Гук высказал предположение, что одной только силы притяжения к Солнцу вполне достаточно для объяснения движения планет, просто нужно предполагать, что планетная орбита является результатом сочетания (суперпозиции) падения на Солнце (благодаря силе притяжения) и движения по инерции (по касательной к траектории планеты). По его мнению, эта суперпозиция движений и обусловливает эллиптическую форму траектории планеты вокруг Солнца. Близкие взгляды, но в достаточно неопределённой форме, высказывал и Кристофер Рен. Гук и Рен догадывались, что сила тяготения убывает обратно пропорционально квадрату расстояния до Солнца.

Однако никто до Ньютона не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера). Более того, именно Ньютон первым догадался, что гравитация действует между двумя любыми телами во Вселенной; движением падающего яблока и вращением Луны вокруг Земли управляет одна и та же сила. Наконец, Ньютон не просто опубликовал предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель:

• закон тяготения;
• закон движения (второй закон Ньютона);
• система методов для математического исследования (математический анализ).

В совокупности эта триада достаточна для полного исследования самых сложных движений небесных тел, тем самым создавая основынебесной механики. Таким образом, только с трудов Ньютона начинается наука динамика, в том числе в применении к движению небесных тел. До создания теории относительности и квантовой механики никаких принципиальных поправок к указанной модели не понадобилось, хотя математический аппарат оказалось необходимым значительно развить.
Первым аргументом в пользу ньютоновской модели послужил строгий вывод на её основе эмпирических законов Кеплера. Следующим шагом стала теория движения комет и Луны, изложенная в «Началах». Позже с помощью ньютоновского тяготения были с высокой точностью объяснены все наблюдаемые движения небесных тел; в этом большая заслугаЭйлера, Клеро и Лапласа, которые разработали для этого теорию возмущений. Фундамент этой теории был заложен ещё Ньютоном, который провёл анализ движения Луны, используя свой обычный метод разложения в ряд; на этом пути он открыл причины известных тогда нерегулярностей (неравенств) в движении Луны.
Закон тяготения позволил решить не только проблемы небесной механики, но и ряд физических и астрофизических задач. Ньютон указал метод определения массы Солнца и планет. Он открыл причину приливов: притяжение Луны (даже Галилей считал приливы центробежным эффектом). Более того, обработав многолетние данные о высоте приливов, он с хорошей точностью вычислил массу Луны. Ещё одним следствием тяготения оказалась прецессия земной оси. Ньютон выяснил, что из-за сплюснутости Земли у полюсов земная ось совершает под действием притяжения Луны и Солнца постоянное медленное смещение с периодом 26000 лет. Тем самым древняя проблема «предварения равноденствий» (впервые отмеченная Гиппархом) нашла научное объяснение.
Ньютоновская теория тяготения вызвала многолетние дебаты и критику принятой в ней концепции дальнодействия. Однако выдающиеся успехи небесной механики в XVIII веке утвердили мнение об адекватности ньютоновской модели. Первые наблюдаемые отклонения от теории Ньютона в астрономии (смещение перигелия Меркурия) были обнаружены лишь через 200 лет. Вскоре эти отклонения объяснила общая теория относительности (ОТО); ньютоновская теория оказалась её приближённым вариантом. ОТО также наполнила теорию тяготения физическим содержанием, указав материальный носитель силы притяжения — метрику пространства-времени, и позволила избавиться от дальнодействия.

Оптика и теория света

Ньютону принадлежат фундаментальные открытия в оптике. Он построил первый зеркальный телескоп (рефлектор), в котором, в отличие от чисто линзовых телескопов, отсутствовалахроматическая аберрация. Он также детально исследовал дисперсию света, показал, что белый свет раскладывается на цвета радуги вследствие различного преломления лучей разных цветов при прохождении через призму, и заложил основы правильной теории цветов. Ньютон создал математическую теорию открытых Гуком интерференционных колец, которые с тех пор получили название «кольца Ньютона». В письме к Флемстиду он изложил подробную теорию астрономической рефракции. Но его главное достижение — создание основ физической (не только геометрической) оптики как науки и разработка её математической базы, превращение теории света из бессистемного набора фактов в науку с богатым качественным и количественным содержанием, экспериментально хорошо обоснованным. Оптические опыты Ньютона на десятилетия стали образцом глубокого физического исследования.
В этот период было множество спекулятивных теорий света и цветности; в основном боролись точка зрения Аристотеля («разные цвета есть смешение света и тьмы в разных пропорциях») и Декарта («разные цвета создаются при вращении световых частиц с разной скоростью»). Гук в своей «Микрографии» (1665) предлагал вариант аристотелевских взглядов. Многие полагали, что цвет есть атрибут не света, а освещённого предмета. Всеобщий разлад усугубил каскад открытий XVII века: дифракция (1665, Гримальди),интерференция (1665, Гук), двойное лучепреломление (1670, Эразм Бартолин, изучено Гюйгенсом), оценка скорости света (1675, Рёмер). Теории света, совместимой со всеми этими фактами, не существовало.

В своём выступлении перед Королевским обществом Ньютон опроверг как Аристотеля, так и Декарта, и убедительно доказал, что белый свет не первичен, а состоит из цветных компонентов с разными углами преломления. Эти-то составляющие и первичны — никакими ухищрениями Ньютон не смог изменить их цвет. Тем самым субъективное ощущение цвета получало прочную объективную базу — показатель преломления.

В 1689 году Ньютон прекратил публикации в области оптики (хотя продолжал исследования) — по распространённой легенде, поклялся ничего не печатать в этой области при жизни Гука. Во всяком случае, в 1704 году, на следующий год после смерти Гука, выходит в свет (на английском языке) монография «Оптика». В предисловии к ней содержится явный намёк на конфликт с Гуком: «Не желая быть втянутым в диспуты по разным вопросам, я оттягивал это издание и задержал бы его и далее, если бы не настойчивость моих друзей». При жизни автора «Оптика», как и «Начала», выдержала три издания (1704, 1717, 1721) и множество переводов, в том числе три на латинском языке.

• Книга первая: принципы геометрической оптики, учение о дисперсии света и составе белого цвета с различными приложениями, включая теорию радуги.
• Книга вторая: интерференция света в тонких пластинках.
• Книга третья: дифракция и поляризация света.

Историки выделяют две группы тогдашних гипотез о природе света.

• Эмиссионная (корпускулярная): свет состоит из мелких частиц (корпускул), излучаемых светящимся телом. В пользу этого мнения говорила прямолинейность распространения света, на которой основана геометрическая оптика, однако дифракция и интерференция плохо укладывались в эту теорию.
• Волновая: свет представляет собой волну в невидимом мировом эфире. Оппонентов Ньютона (Гука, Гюйгенса) нередко называют сторонниками волновой теории, однако надо иметь в виду, что под волной они понимали не периодическое колебание, как в современной теории, а одиночный импульс; по этой причине их объяснения световых явлений были мало правдоподобны и не могли составить конкуренцию ньютоновским (Гюйгенс даже пытался опровергнуть дифракцию). Развитая волновая оптика появилась только в начале XIX века.
  Ньютона часто считают сторонником корпускулярной теории света; на самом деле он, по своему обыкновению, «гипотез не измышлял» и охотно допускал, что свет может быть связан и с волнами в эфире. В трактате, представленном в Королевское общество в 1675 году, он пишет, что свет не может быть просто колебаниями эфира, так как тогда он, например, мог бы распространяться по изогнутой трубе, как это делает звук. Но, с другой стороны, он предлагает считать, что распространение света возбуждает колебания в эфире, что и порождает дифракцию и другие волновые эффекты. По существу, Ньютон, ясно сознавая достоинства и недостатки обоих подходов, выдвигает компромиссную, корпускулярно-волновую теорию света. В своих работах Ньютон детально описал математическую модель световых явлений, оставляя в стороне вопрос о физическом носителе света: «Учение моё о преломлении света и цветах состоит единственно в установлении некоторых свойств света без всяких гипотез о его происхождении». Волновая оптика, когда она появилась, не отвергла модели Ньютона, а вобрала их в себя и расширила на новой основе.
  Несмотря на свою нелюбовь к гипотезам, Ньютон поместил в конце «Оптики» список нерешённых проблем и возможных ответов на них. Впрочем, в эти годы он уже мог себе такое позволить —— авторитет Ньютона после «Начал» стал непререкаемым, и докучать ему возражениями уже мало кто решался. Ряд гипотез оказались пророческими. В частности, Ньютон предсказал:
  отклонение света в поле тяготения;
  явление поляризации света;
  взаимопревращение света и вещества.
  

Галилео Галилей

Галилео Галилей — итальянский физик, механик, астроном,философ и математик, оказавший значительное влияние на науку своего времени. Он первым использовал телескоп для наблюдения небесных тел и сделал ряд выдающихся астрономических открытий.

Биография

Галилей родился в 1564 году в итальянском городе Пиза, в семье родовитого, но обедневшего дворянина Винченцо Галилея, видного теоретика музыки и лютниста. Полное имя Галилео Галилея: Галилео ди Винченцо Бонайути де Галилей (итал. Galileo di Vincenzo Bonaiuti de' Galilei). Представители рода Галилеев упоминаются в документах с XIV века. Несколько его прямых предков были приорами (членами правящего совета) Флорентийской республики, а прапрадед Галилея, известный врач, тоже носивший имя Галилео, в 1445 году был избран главой республики.
В семье Винченцо Галилея и Джулии Амманнати было шестеро детей, но выжить удалось четверым: Галилео (старшему из детей), дочерям Вирджинии, Ливии и младшему сыну Микеланджело, который в дальнейшем тоже приобрел известность как композитор-лютнист. В 1572 году Винченцо переехал во Флоренцию, столицу Тосканского герцогства. Правящая там династия Медичи была известна широким и постоянным покровительством искусству и наукам.
О детстве Галилея известно немного. С ранних лет мальчика влекло к искусству; через всю жизнь он пронёс любовь к музыке и рисованию, которыми владел в совершенстве. В зрелые годы лучшие художники Флоренции — Чиголи, Бронзино и др. — советовались с ним о вопросах перспективы и композиции; Чиголи даже утверждал, что именно Галилею он обязан своей славой. По сочинениям Галилея можно сделать также вывод о наличии у него замечательного литературного таланта.
Начальное образование Галилей получил в расположенном неподалёку монастыре Валломброза. Мальчик очень любил учиться и стал одним из лучших учеников в классе. Он взвешивал возможность стать священником, но отец был против.


Здание Пизанского университета (в наши дни — Высшая Нормальная школа)
В 1581 году 17-летний Галилей по настоянию отца поступил в Пизанский университет изучать медицину. В университете Галилей посещал также лекции по геометрии (ранее он с математикой был совершенно не знаком) и настолько увлёкся этой наукой, что отец стал опасаться, как бы это не помешало изучению медицины.
Галилей пробыл студентом неполных три года; за это время он успел основательно ознакомиться с сочинениями античных философов и математиков и заработал среди преподавателей репутацию неукротимого спорщика. Уже тогда он считал себя вправе иметь собственное мнение по всем научным вопросам, не считаясь с традиционными авторитетами.
Вероятно, в эти годы он познакомился с теорией Коперника. Астрономические проблемы тогда живо обсуждались, особенно в связи с только что проведённой календарной реформой.


Маркиз Гвидобальдо дель Монте
Вскоре финансовое положение отца ухудшилось, и он оказался не в состоянии оплачивать далее обучение сына. Просьба освободить Галилея от платы (такое исключение делалось для самых способных студентов) была отклонена. Галилей вернулся во Флоренцию (1585), так и не получив учёной степени. К счастью, он успел обратить на себя внимание несколькими остроумными изобретениями (например, гидростатическими весами), благодаря чему познакомился с образованным и богатым любителем науки, маркизом Гвидобальдо дель Монте. Маркиз, в отличие от пизанских профессоров, сумел его правильно оценить. Уже тогда дель Монте говорил, что со времени Архимеда мир не видел такого гения, как Галилей[3]. Восхищённый необыкновенным талантом юноши, маркиз стал его другом и покровителем; он представил Галилея тосканскому герцогу Фердинанду I Медичи и ходатайствовал об оплачиваемой научной должности для него.
В 1589 году Галилей вернулся в Пизанский университет, теперь уже профессором математики. Там он начал проводить самостоятельные исследования по механике и математике. Правда, жалованье ему назначили минимальное: 60 скудо в год (профессор медицины получал 2000 скудо). В 1590 году Галилей написал трактат «О движении».
В 1591 году умер отец, и ответственность за семью перешла к Галилео. В первую очередь он должен был позаботиться о воспитании младшего брата и о приданом двух незамужних сестёр.
В 1592 году Галилей получил место в престижном и богатом Падуанском университете (Венецианская республика), где преподавал астрономию, механику и математику. По рекомендательному письму венецианского дожа университету можно судить о том, что научный авторитет Галилея уже в эти годы был чрезвычайно высок:

Сознавая всю важность математических знаний и их пользу для других главных наук, мы медлили назначением, не находя достойного кандидата. В настоящее время заявил желание занять это место синьор Галилей, бывший профессор в Пизе, пользующийся большой известностью и справедливо признаваемый за самого сведущего в математических науках. Поэтому мы с удовольствием предоставляем ему кафедру математики на четыре года со 180 флоринами жалованья в год.

Философия и научный метод

Хотя в древней Греции были замечательные инженеры (Архимед, Герон и другие), сама идея экспериментального метода познания, который должен дополнять и подтверждать дедуктивно-умозрительные построения, была чужда аристократическому духу античной физики. В Европе ещё в XIII веке Роберт Гроссетест и Роджер Бэкон призвали к созданию экспериментальной науки, которая на математическом языке сможет описать природные явления, однако до Галилея в реализации этой идеи не было существенного продвижения: научные методы мало отличались от теологических, и ответы на научные вопросы по-прежнему искали в книгах древних авторитетов. Научная революция в физике начинается с Галилея.
В отношении философии природы Галилей был убеждённым рационалистом. Он считал, что законы природы постижимы для человеческого разума. В «Диалоге о двух системах мира» он писал:

Я утверждаю, что человеческий разум познаёт некоторые истины столь совершенно и с такой абсолютной достоверностью, какую имеет сама природа; таковы чистые математические науки, геометрия и арифметика; хотя Божественный разум знает в них бесконечно больше истин… но в тех немногих, которые постиг человеческий разум, я думаю, его познание по объективной достоверности равно Божественному, ибо оно приходит к пониманию их необходимости, а высшей степени достоверности не существует.

Разум у Галилея — сам себе судья; в случае конфликта с любым другим авторитетом, даже религиозным, он не должен уступать:

Мне кажется, что при обсуждении естественных проблем мы должны отправляться не от авторитета текстов Священного Писания, а от чувственных опытов и необходимых доказательств… Я полагаю, что всё касающееся действий природы, что доступно нашим глазам или может быть уяснено путём логических доказательств, не должно возбуждать сомнений, ни тем более подвергаться осуждению на основании текстов Священного Писания, может быть, даже превратно понятых.
Бог не менее открывается нам в явлениях природы, нежели в речениях Священного Писания… Было бы опасно приписывать Священному Писанию какое-либо суждение, хотя бы один раз оспоренное опытом

Античные и средневековые философы предлагали для объяснения явлений природы разнообразные «метафизические сущности» (субстанции), которым приписывались надуманные свойства. Галилея такой подход не устраивал

Поиск сущности я считаю занятием суетным и невозможным, а затраченные усилия — в равной мере тщетными как в случае с удалёнными небесными субстанциями, так и с ближайшими и элементарными; и мне кажется, что одинаково неведомы как субстанция Луны, так и Земли, как пятен на Солнце, так и обыкновенных облаков… [Но] если тщетно искать субстанцию солнечных пятен, это ещё не значит, что нами не могут быть исследованы некоторые их характеристики, например место, движение, форма, величина, непрозрачность, способность к изменениям, их образование и исчезновение.

Декарт отверг такую позицию (в его физике основное внимание уделялось именно нахождению «главных причин»), однако начиная с Ньютона галилеевский подход становится преобладающим.
Галилей считается одним из основателей механицизма. Этот научный подход рассматривает Вселенную как гигантский механизм, а сложные природные процессы — как комбинации простейших причин, главная из которых — механическое движение. Анализ механического движения лежит в основе работ Галилея. Он писал в «Пробирных дел мастере»:

Никогда я не стану от внешних тел требовать чего-либо иного, чем величина, фигура, количество, и более или менее быстрые движения для того, чтобы объяснить возникновение ощущений вкуса, запаха и звука; я думаю, что если бы мы устранили уши, языки, носы, то остались бы только фигуры, числа, движения, но не запахи, вкусы и звуки, которые, по моему мнению, вне живого существа являются не чем иным, как только пустыми именами.

Для проектирования эксперимента и для осмысления его результатов нужна некоторая предварительная теоретическая модель исследуемого явления, и основой её Галилей считал математику, выводы которой он рассматривал как самое достоверное знание: книга природы «написана на языке математики»; «Тот, кто хочет решать вопросы естественных наук без помощи математики, ставит неразрешимую задачу. Следует измерять то, что измеримо, и делать измеримым то, что таковым не является.»
Опыт Галилей рассматривал не как простое наблюдение, а как осмысленный и продуманный вопрос, заданный природе. Он допускал и мысленные эксперименты, если их результаты не вызывают сомнений. При этом он ясно представлял, что сам по себе опыт не даёт достоверного знания, и полученный от природы ответ должен подвергнуться анализу, результат которого может привести к переделке исходной модели или даже к замене её на другую. Таким образом, эффективный путь познания, по мнению Галилея, состоит в сочетании синтетического (в его терминологии, композитивный метод) и аналитического (резолютивный метод), чувственного и абстрактного. Эта позиция, поддержанная Декартом, с этого момента утвердилась в науке. Тем самым наука получила свой метод, собственный критерий истины и светский характер.

Механика

Физика и механика в те годы изучались по сочинениям Аристотеля, которые содержали метафизические рассуждения о «первопричинах» природных процессов. В частности, Аристотель утверждал:
• Скорость падения пропорциональна весу тела.
• Движение происходит, пока действует «побудительная причина» (сила), и в отсутствие силы прекращается.
Находясь в Падуанском университете, Галилей изучал инерцию и свободное падение тел. В частности, он заметил, что ускорение свободного падения не зависит от веса тела, таким образом опровергнув первое утверждение Аристотеля.
В своей последней книге Галилей сформулировал правильные законы падения: скорость нарастает пропорционально времени, а путь — пропорционально квадрату времени. В соответствии со своим научным методом он тут же привёл опытные данные, подтверждающие открытые им законы. Более того, Галилей рассмотрел (в 4-й день «Бесед») и обобщённую задачу: исследовать поведение падающего тела с ненулевой горизонтальной начальной скоростью. Он совершенно правильно предположил, что полёт такого тела будет представлять собой суперпозицию (наложение) двух «простых движений»: равномерного горизонтального движения по инерции и равноускоренного вертикального падения.
Галилей доказал, что указанное, а также любое брошенное под углом к горизонту тело летит по параболе. В истории науки это первая решённая задача динамики. В заключение исследования Галилей доказал, что максимальная дальность полёта брошенного тела достигается для угла броска 45° (ранее это предположение высказал Тарталья, который, однако, не смог его строго обосновать). На основе своей модели Галилей (ещё в Венеции) составил первые артиллерийские таблицы.
Галилей опроверг и второй из приведённых законов Аристотеля, сформулировав первый закон механики (закон инерции): при отсутствии внешних сил тело либо покоится, либо равномерно движется. То, что мы называем инерцией, Галилей поэтически назвал «неистребимо запечатлённое движение». Правда, он допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Правильную формулировку закона позднее дали Декарт и Ньютон; тем не менее общепризнанно, что само понятие «движение по инерции» впервые введено Галилеем, и первый закон механики по справедливости носит его имя.
Галилей является одним из основоположников принципа относительности в классической механике, ставшего в слегка уточнённом виде одним из краеугольных камней современной трактовки этой науки и названного позже в его честь. В «Диалоге о двух системах мира» Галилей сформулировал принцип относительности следующим образом:

Для предметов, захваченных равномерным движением, это последнее как бы не существует и проявляет своё действие только на вещах, не принимающих в нём участия.

Разъясняя принцип относительности, Галилей вкладывает в уста Сальвиати обстоятельное и красочное (весьма типичное для стиля научной прозы великого итальянца) описание воображаемого «опыта», проводимого в трюме корабля:

... Запаситесь мухами, бабочками и другими подобными мелкими летающими насекомыми; пусть будет у вас там также большой сосуд с водой и плавающими в нём маленькими рыбками; подвесьте, далее, наверху ведёрко, из которого вода будет падать капля за каплей в другой сосуд с узким горлышком, подставленный внизу. Пока корабль стоит неподвижно, наблюдайте прилежно, как мелкие летающие животные с одной и той же скоростью движутся во все стороны помещения; рыбы, как вы увидите, будут плавать безразлично во всех направлениях; все падающие капли попадут в подставленный сосуд... Заставьте теперь корабль двигаться с малой скоростью и тогда (если только движение будет равномерным и без качки в ту и другую сторону) во всех названных явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно.

Строго говоря, корабль Галилея движется не прямолинейно, а по дуге большого круга поверхности земного шара. В рамках современного понимания принципа относительности система отсчёта, связанная с этим кораблём, будет лишь приближённо инерциальной, так что выявить факт его движения, не обращаясь к внешним ориентирам, всё же возможно (правда, пригодные для этого измерительные приборы появились лишь в XX веке...).Перечисленные выше открытия Галилея, кроме всего прочего, позволили ему опровергнуть многие доводы противников гелиоцентрической системы мира, утверждавших, что вращение Земли заметно сказалось бы на явлениях, происходящих на её поверхности. Например, по мнению геоцентристов, поверхность вращающейся Земли за время падения любого тела уходила бы из-под этого тела, смещаясь на десятки или даже сотни метров. Галилей уверенно предсказал: «Будут безрезультатны любые опыты, которые должны были бы указывать более против, чем за вращение Земли».Галилей опубликовал исследование колебаний маятника и заявил, что период колебаний не зависит от их амплитуды (это приблизительно верно для малых амплитуд). Он также обнаружил, что периоды колебаний маятника соотносятся как квадратные корни из его длины. Результаты Галилея привлекли внимание Гюйгенса, который изобрёл часы с маятниковым регулятором (1657); с этого момента появилась возможность точных измерений в экспериментальной физике.Впервые в истории науки Галилей поставил вопрос о прочности стержней и балок при изгибе и тем самым положил начало новой науке — сопротивлению материалов.Многие рассуждения Галилея представляют собой наброски открытых много позднее физических законов. Например, в «Диалоге» он сообщает, что вертикальная скорость шара, катящегося по поверхности сложного рельефа, зависит только от его текущей высоты, и иллюстрирует этот факт несколькими мысленными экспериментами; сейчас мы бы сформулировали этот вывод как закон сохранения энергии в поле тяжести. Аналогично он объясняет (теоретически незатухающие) качания маятника.В статике Галилей ввёл фундаментальное понятие момента силы (итал. momento).

Гей-Люссак Жозеф Луи

Биография

Французский физик и химик Жозеф Луи Гей-Люссак родился в Сен-Леонар-де-Нобла (департамент Верхняя Вьенна). Получив в детстве строгое католическое воспитание, в 15 лет он переехал в Париж; там, в пансионе Сансье, юноша продемонстрировал незаурядные математические способности. В 1797-1800 гг. Гей-Люссак учился в Политехнической школе в Париже, где химию преподавал Клод Луи Бертолле. После окончания школы Гей-Люссак был ассистентом Бертолле. В 1809 г. он почти одновременно стал профессором химии в Политехнической школе и профессором физики в Сорбонне, а с 1832 г. – ещё и профессором химии Парижского ботанического сада.

Научные работы Гей-Люссака относятся к самым разным областям химии. В 1802 г. независимо от Джона Дальтона Гей-Люссак открыл один из газовых законов – закон теплового расширения газов, позже названный его именем. В 1804 г. он совершил два полёта на воздушном шаре (поднявшись на высоту 4 и 7 км), во время которых выполнил ряд научных исследований, в частности измерил температуру и влажность воздуха. В 1805 г. совместно с немецким естествоиспытателем Александром фон Гумбольдтом установил состав воды, показав, что соотношение водорода и кислорода в её молекуле равно 2:1. В 1808 г. Гей-Люссак открыл закон объёмных отношений, который представил на заседании Философско-математического общества: «При взаимодействии газов их объёмы и объёмы газообразных продуктов соотносятся как простые числа». В 1809 г. он провел серию опытов с хлором, подтвердивших вывод Гэмпфри Дэви, что хлор – это элемент, а не кислородсодержащее соединение, а в 1810 г. установил элементарный характер калия и натрия, затем фосфора и серы. В 1811 г. Гей-Люссак совместно в французским химиком-аналитиком Луи Жаком Тенаром значительно усовершенствовал метод элементного анализа органических веществ.

В 1811 г. Гей-Люссак начал обстоятельное исследование синильной кислоты, установил её состав и провёл аналогию между нею, галогеноводородными кислотами и сероводородом. Полученные результаты привели его к концепции водородных кислот, опровергающей чисто кислородную теорию Антуана Лорана Лавуазье. В 1811-1813 гг. Гей-Люссак установил аналогию между хлором и иодом, получил иодистоводородную и иодную кислоты, монохлорид иода. В 1815 г. он получил и изучил «циан» (точнее говоря, дициан), что послужило одной из предпосылок формирования теории сложных радикалов.

Гей-Люссак работал во многих государственных комиссиях и составлял по поручению правительства доклады с рекомендациями по внедрению научных достижений в промышленность. Прикладное значение имели и многие его исследования. Так, его метод определения содержания этилового спирта был положен в основу практических способов определения крепости алкогольных напитков. Гей-Люссак разработал в 1828 г. методику титриметрического определения кислот и щелочей, а 1830 г. – объёмный способ определения серебра в сплавах, применяющийся и в настоящее время. Созданная им конструкция башни для улавливания оксидов азота в дальнейшем нашла применение в производстве серной кислоты. В 1825 г. Гей-Люссак совместно с Мишелем Эженом Шеврёлем получили патент на производство стеариновых свечей.

В 1806 г. Гей-Люссак был избран членом Французской академии наук и её президентом в 1822 и 1834 гг.; состоял членом Аркёйского научного общества (Societe d'Archueil), основанного Бертолле. В 1839 г. он получил титул пэра Франции.

Карл Фридрих Гаусс

Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген) — немецкий математик, механик, физик, астроном и геодезист. Считается одним из величайших математиков всех времён, «королём математиков». Лауреат медали Копли (1838), иностранный член Шведской (1821) и Российской (1824) Академий наук, английского Королевского общества.

Биография

1777—1798 годы

Дед Гаусса был бедным крестьянином, отец — садовником, каменщиком, смотрителем каналов в герцогстве Брауншвейг. Уже в двухлетнем возрасте мальчик показал себя вундеркиндом. В три года он умел читать и писать, даже исправлял счётные ошибки отца. Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 50 * 101=5050.

До самой старости он привык большую часть вычислений производить в уме.

С учителем ему повезло: М. Бартельс (впоследствии учитель Лобачевского) оценил исключительный талант юного Гаусса и сумел выхлопотать ему стипендию от герцога Брауншвейгского. Это помогло Гауссу закончить колледж Collegium Carolinum в Брауншвейге (1792—1795).

Свободно владея множеством языков, Гаусс некоторое время колебался в выборе между филологией и математикой, но предпочёл последнюю. Он очень любил латинский язык и значительную часть своих трудов написал на латыни; любил английскую, французскую и русскую литературу. В возрасте 62 лет Гаусс начал изучать русский язык, чтобы ознакомиться с трудами Лобачевского, и вполне преуспел в этом деле.

В колледже Гаусс изучил труды Ньютона, Эйлера, Лагранжа. Уже там он сделал несколько открытий в теории чисел, в том числе доказал закон взаимности квадратичных вычетов. Лежандр, правда, открыл этот важнейший закон раньше, но строго доказать не сумел; Эйлеру это также не удалось. Кроме этого, Гаусс создал «метод наименьших квадратов» (тоже независимо открытый Лежандром) и начал исследования в области «нормального распределения ошибок».

С 1795 по 1798 год Гаусс учился в Гёттингенском университете, где его учителем был А. Г. Кестнер. Это — наиболее плодотворный период в жизни Гаусса.

1796 год: Гаусс доказал возможность построения с помощью циркуля и линейки правильного семнадцатиугольника. Более того, он разрешил проблему построения правильных многоугольников до конца и нашёл критерий возможности построения правильного n-угольника с помощью циркуля и линейки: если n — простое число, то оно должно быть вида 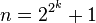(числом Ферма). Этим открытием Гаусс очень дорожил и завещал изобразить на его могиле правильный 17-угольник, вписанный в круг.

С 1796 года Гаусс ведёт краткий дневник своих открытий. Многое он, подобно Ньютону, не публиковал, хотя это были результаты исключительной важности (эллиптические функции, неевклидова геометрия и др.). Своим друзьям он пояснял, что публикует только те результаты, которыми доволен и считает завершёнными. Многие отложенные или заброшенные им идеи позже воскресли в трудах Абеля, Якоби, Коши, Лобачевского и др. Кватернионы он тоже открыл за 30 лет до Гамильтона (назвав их «мутациями»).

Все многочисленные опубликованные труды Гаусса содержат значительные результаты, сырых и проходных работ не было ни одной.

1798 год: закончен шедевр «Арифметические исследования» (лат. Disquisitiones Arithmeticae), напечатан только в 1801 году.

В этом труде подробно излагается теория сравнений в современных (введённых им) обозначениях, решаются сравнения произвольного порядка, глубоко исследуются квадратичные формы, комплексные корни из единицы используются для построения правильных n-угольников, изложены свойства квадратичных вычетов, приведено доказательство квадратичного закона взаимности и т. д. Гаусс любил говорить, что математика — царица наук, а теория чисел — царица математики.

1798—1816 годы

В 1798 году Гаусс вернулся в Брауншвейг и жил там до 1807 года.

Герцог продолжал опекать молодого гения. Он оплатил печать его докторской диссертации (1799) и пожаловал неплохую стипендию. В своей докторской Гаусс впервые доказал основную теорему алгебры. До Гаусса было много попыток это сделать, наиболее близко к цели подошёл Д'Аламбер. Гаусс неоднократно возвращался к этой теореме и дал 4 различных её доказательства.

С 1799 года Гаусс — приват-доцент Брауншвейгского университета.

1801 год: избирается членом-корреспондентом Петербургской Академии наук.

После 1801 года Гаусс, не порывая с теорией чисел, расширил круг своих интересов, включив в него и естественные науки. Катализатором послужило открытие малой планеты Церера (1801), потерянной вскоре после обнаружения. 24-летний Гаусс проделал (за несколько часов) сложнейшие вычисления, пользуясь разработанным им же новым вычислительным методом, и с большой точностью указал место, где искать «беглянку»; там она, к общему восторгу, и была вскоре обнаружена.

Слава Гаусса становится общеевропейской. Многие научные общества Европы избирают Гаусса своим членом, герцог увеличивает пособие, а интерес Гаусса к астрономии ещё более возрастает.

1805 год: Гаусс женился на Иоганне Остгоф. У них было трое детей.

1806 год: от раны, полученной на войне с Наполеоном, умирает его великодушный покровитель-герцог. Несколько стран наперебой приглашают Гаусса на службу (в том числе в Петербург). По рекомендации Александра фон Гумбольдта Гаусса назначают профессором в Гёттингене и директором Гёттингенской обсерватории. Эту должность он занимал до самой смерти.

1807 год: наполеоновские войска занимают Гёттинген. Все граждане облагаются контрибуцией, в том числе огромную сумму — 2000 франков — требуется заплатить Гауссу. Ольберс и Лаплас тут же приходят ему на помощь, но Гаусс отклоняет их деньги; тогда неизвестный из Франкфурта присылает ему 1000 гульденов, и этот дар приходится принять. Только много позднее узнали, что неизвестным был курфюрст Майнцский, друг Гёте.

1809 год: новый шедевр, «Теория движения небесных тел». Изложена каноническая теория учёта возмущений орбит.

Как раз в четвёртую годовщину свадьбы умирает Иоганна, вскоре после рождения третьего ребёнка. В Германии разруха и анархия. Это самые тяжёлые годы для Гаусса.

1810 год: новая женитьба, на Минне Вальдек, подруге Иоганны. Число детей Гаусса вскоре увеличивается до шести.

1810 год: новые почести. Гаусс получает премию Парижской академии наук и золотую медаль Лондонского королевского общества.

1811 год: появляется новая комета. Гаусс быстро и очень точно рассчитывает её орбиту. Начинает работу над комплексным анализом, открывает (но не публикует) теорему, позже переоткрытую Коши и Вейерштрассом: интеграл от аналитической функции по замкнутому контуру равен нулю.

1812 год: исследование гипергеометрического ряда, обобщающего разложение практически всех известных тогда функций.

Знаменитую комету «пожара Москвы» (1812) всюду наблюдают, пользуясь вычислениями Гаусса.

1815 год: публикует первое строгое доказательство основной теоремы алгебры.

1816—1855 годы

1820 год: Гауссу поручают произвести геодезическую съёмку Ганновера. Для этого он разработал соответствующие вычислительные методы (в т. ч. методику практического применения своего метода наименьших квадратов), приведшие к созданию нового научного направления — высшей геодезии, и организовал съёмку местности и составление карт.

1821 год: в связи с работами по геодезии Гаусс начинает исторический цикл работ по теории поверхностей. В науку входит понятие «гауссовой кривизны». Положено начало дифференциальной геометрии. Именно результаты Гаусса вдохновили Римана на написание его классической диссертации о «римановой геометрии».

Итогом изысканий Гаусса была работа «Исследования относительно кривых поверхностей» (1822). В ней свободно использовались общие криволинейные координаты на поверхности. Гаусс далеко развил метод конформного отображения, которое в картографии сохраняет углы (но искажает расстояния); оно применяется также в аэро-, гидродинамике и электростатике.

1824 год: избирается иностранным почётным членом Петербургской Академии наук.

1825 год: открывает гауссовы комплексные целые числа, строит для них теорию делимости и сравнений. Успешно применяет их для решения сравнений высоких степеней.

1829 год: в замечательной работе «Об одном новом общем законе механики», состоящей всего из четырёх страниц, Гаусс обосновывает новый вариационный принцип механики — принцип наименьшего принуждения. Принцип применим к механическим системам с идеальными связями и сформулирован Гауссом так: «движение системы материальных точек, связанных между собой произвольным образом и подверженных любым влияниям, в каждое мгновение происходит в наиболее совершенном, какое только возможно, согласии с тем движением, каким обладали бы эти точки, если бы все они стали свободными, т. е. происходит с наименьшим возможным принуждением, если в качестве меры принуждения, применённого в течение бесконечно малого мгновения, принять сумму произведений массы каждой точки на квадрат величины её отклонения от того положения, которое она заняла бы, если бы была свободной».

1831 год: умирает вторая жена, у Гаусса начинается тяжелейшая бессонница. В Гёттинген приезжает приглашённый по инициативе Гаусса 27-летний талантливый физик Вильгельм Вебер, с которым Гаусс познакомился в 1828 году, в гостях у Гумбольдта. Оба энтузиаста науки сдружились, несмотря на разницу в возрасте, и начинают цикл исследований электромагнетизма.

1832 год: «Теория биквадратичных вычетов». С помощью тех же целых комплексных гауссовых чисел доказываются важные арифметические теоремы не только для комплексных, но и для вещественных чисел. Здесь же Гаусс приводит геометрическую интерпретацию комплексных чисел, которая с этого момента становится общепринятой.

1833 год: Гаусс изобретает электрический телеграф и (вместе с Вебером) строит его действующую модель.

1837 год: Вебера увольняют за отказ принести присягу новому королю Ганновера. Гаусс вновь остаётся в одиночестве.

1839 год: 62-летний Гаусс овладевает русским языком и в письмах в Петербургскую Академию просил прислать ему русские журналы и книги, в частности «Капитанскую дочку» Пушкина. Предполагают, что это связано с интересом Гаусса к работам Лобачевского, который в 1842 году по рекомендации Гаусса был избран иностранным членом-корреспондентом Гёттингенского королевского общества.

В том же 1839 году Гаусс в сочинении «Общая теория сил притяжения и отталкивания, действующих обратно пропорционально квадрату расстояния» изложил основы теории потенциала, включая ряд основополагающих положений и теорем — например, основную теорему электростатики (теорема Гаусса).

1840 год: в работе «Диоптрические исследования» Гаусс разработал теорию построения изображений в сложных оптических системах.

Умер Гаусс 23 февраля 1855 года в Гёттингене.

Современники вспоминают Гаусса как жизнерадостного, дружелюбного человека, с отличным чувством юмора.

Юстус фон Либих

Юстус фон Либих (нем. Justus von Liebig; 12 мая 1803, Дармштадт — 18 апреля 1873, Мюнхен) — немецкий ученый, внес значительный вклад в развитие органической химии, один из основателей агрохимии и создателей системы химического образования.

Биография

Первоначальное образование получил в дармштадтской гимназии. Университетское образование получил в Бонне и Эрлангене (1819—1822).

В 1822 г. переехал в Париж, где благодаря своей научной работе, представленной французской академии наук, стал известен Александру Гумбольдту, с помощью которого познакомился с Гей-Люссаком. Либих уже с 1824 г. стал экстраординарным, а с 1826 г. и ординарным профессором химии в Гессене.

Благодаря своим необыкновенным дарованиям Либих скоро стал главой научной школы. При поддержке правительства им была устроена первая в Германии образцовая лаборатория, которая более четверти столетия привлекала учёных всех стран.

Многие из русских учёных были учениками Либиха, как напр. А. Воскресенский, Н. Зинин, А. Ходнев, П. Ильенков, Н. Соколов, К. Шмидт. Либих великим герцогом гессенским произведён в бароны. С 1852 г. состоял профессором в мюнхенском университете, с 1860 г. — президент академии наук и главный консерватор научных музеев государства.

В Дармштадте ему поставлен памятник в 1887 г.; в Гессене в 1890 г. и ещё ранее, в 1883 г., немецкое химическое общество воздвигло ему памятник на Максимилиановской площади в Мюнхене. Нельзя не удивляться разнообразию, многочисленности и плодотворности работ Либиха.

Изданная им в 1840 г. (9 издание в 1876 г.), «Die organische Chemie in ihrer Anwendung auf Agrikultur und Physiologie» была, по справедливому выражению Гофмана, благодеянием для человечества. Его «Naturwissensch. Briefe uber die moderne Landwirtschaft» (Лпц., 1859 г.) не только интересны для химии, но и для остальных отраслей естествознания. В ней автор предлагает теорию минерального питания растений и дал рекомендации повышения урожайности путем внесения минеральных удобрений в почву.

Не менее известны его «Die organische Chemie in ihrer Anwendung auf Physiologie und Pathologie» (1842, 3 изд. 1846 г.). Эти работы переведены на французский, английский, итальянский, венгерский и русский языки. Из других капитальных сочинений укажем на «Theorie und Praxis in der Landwirtschaft» (1856). Кроме большого числа научных работ, указанных ниже, Либих редактировал «Annalen der Chemie und Pharmacie», издаваемый им с 1832 г. совместно с Гейгером, с 1851 — с Велером и Коппом.

Совместно с Поггендорфом им начато издание «Handworterbuch der Chemie», и кроме того им была обработана химическая часть в «Учебнике фармации» Гейгера, органическая часть которого вышла как самостоятельный «Учебник химии» (1839—1843). Научные работы Либиха также касаются всех отраслей этой науки.

Юстус Либих умер 18 апреля 1873 года и похоронен на Старом южном кладбище в Мюнхене.

Научный вклад

В технической и агрономической химии важны его исследования над цианистым калием в применении его к фабрикации жёлтой кровяной соли и гальванопластике, работы об альдегидах при фабрикации уксуса, опыты над серебрением стекла для фабрикации зеркал, над известковыми суперфосфатами в применении к земледелию.

В области аналитической химии заслуживают большого внимания работы, касающиеся метода отделения никеля от кобальта, метода определения кислорода воздуха при помощи пирогалловой кислоты, а также определение соли и мочевины в моче человека и хищных животных.

Главная заслуга Либиха несомненно, однако, принадлежит к области органической химии. Он усовершенствовал аппарат для сжигания органических соединений (печь Либиха) и улучшил метод анализа; исследовал почти все важнейшие органические кислоты; изучил продукты разложения спирта хлором, продукты окисления алкоголя и сверх того составные части жидкостей мяса. Либих открыл в аммелине и меламине первые могущие быть искусственно приготовленными углеродосодержащие основания, нашёл в моче сначала травоядных, а потом человека — гиппуровую кислоту, в жидкости мяса — креатинин и инозиновую кислоту и тирозин как продукт разложения казеина. Он отличил далее цинтонин — главную составную часть вещества мускулов — от кровяного фибрина. С Велером Либих предпринял исследование циановой и мочевой кислот, радикала бензойной кислоты и масла горьких миндалей.

Либих открыл один из фундаментальных законов экологии — закон ограничивающего фактора (известный также, как бочка Либиха).

Либих также известен и как оратор. Между речами, сказанными им как президентом академии, следует указать речь «О Фрэнсисе Бэконе Веруламском» (1863), «Индукция и дедукция» (1865), одна из позднейших — «Развитие идей естествознания».

Аполлоний Пергский

Аполлоний Пергский (262 до н. э. — 190 до н. э.) — древнегреческий математик, один из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н. э.

Аполлоний прославился в первую очередь монографией «Конические сечения» (8 книг), в которой дал содержательную общую теорию эллипса, параболы и гиперболы. Именно Аполлоний предложил общепринятые названия этих кривых; до него их называли просто «сечениями конуса». Он ввёл и другие математические термины, латинские аналоги которых навсегда вошли в науку, в частности: асимптота, абсцисса, ордината, аппликата.

Из других заслуг Аполлония перед наукой отметим, что он переработал астрономическую модель Евдокса, введя эпициклы и эксцентрики для объяснения неравномерности движения планет. Эту теорию позднее развили Гиппарх и Птолемей. Он также дал решение задачи о построении окружности, касающейся трёх заданных окружностей («задача Аполлония»), изучал спиральные линии, занимался геометрической оптикой.

В честь Аполлония назван кратер на Луне.

Труд о конических сечениях

Четыре книги главного сочинения Аполлония о конических сечениях дошли до нас в греческом оригинале, три — в арабском переводе Сабита ибн Курры, а 8-я потеряна. Эдмонд Галлей подготовил образцовое издание данного труда (Оксфорд, 1710), куда включил свою попытку реконструкции VIII книги (на основании предисловия к VII книге). До Галлея аналогичную попытку предпринял Ибн ал-Хайсам.

Предшественниками Аполлония были Менехм, Конон Самосский, а также Евклид, чьё сочинение «Начала конических сечений» до нас не дошло. Евклид не включил теорию конических сечений в свои «Начала», вероятно, по той причине, что античные математики считали «совершенными линиями» только прямые и окружности.

В книге I приводятся определения и уравнения («симптомы») конических сечений — впрочем, известные и до Аполлония. Новым явилось то, что классификация кривых, как и в современных учебниках, проводится алгебраически — по виду уравнения, а не из геометрических соображений. Более того, Аполлоний строго доказывает, что вид уравнения не зависит от выбора опорной системы координат; в качестве таковой выступают, как правило, произвольный диаметр кривой и касательная в одном из концов диаметра, но Аполлоний рассматривает и другие косоугольные системы координат (например, для гиперболы — пара асимптот).

В последующем изложении (книги II—IV) выясняются свойства особых точек и линий, связанных с исследуемой кривой: фокусов, асимптот, полюсов и поляр, перечисляются их свойства, доказывается, что конические сечения могут пересекаться не более чем в 4 точках, поясняется, как строить касательные к этим кривым, определяются площади сегментов. Всего в труде 387 теорем.

В предисловии Аполлоний сообщает, что, начиная с III книги, бо?льшая часть теорем являются новыми.

V книга: теория нормалей и эволют для конических сечений, задачи на максимум и минимум.

VI книга: теория подобия конических сечений.

В VII-й (и, видимо, в VIII-й) книге приводятся знаменитые теоремы Аполлония о сопряжённых диаметрах и разнообразные приложения теории к геометрическим задачам.

Большой интерес представляют не только результаты Аполлония, но и методы, которыми он пользуется. В них можно найти многочисленные мотивы более поздних достижений математики — алгебры, аналитической, проективной геометрии и местами даже дифференциальной геометрии.

Книга оказала огромное влияние на творчество последующих математиков, включая Ферма, Декарта, Ньютона, Лагранжа и многих других. Многие теоремы Аполлония, особенно о максимумах, эволютах, нормалях и т. п. вошли в современные учебники по дифференциальной геометрии конических сечений.

Каким образом Аполлоний, не владея математическим анализом, сумел сделать свои открытия, неясно. Возможно, у него, как у Архимеда, был некий метод бесконечно малых, который он использовал в эвристических целях, чтобы затем передоказать результат каноническими средствами античной геометрии. Ван дер Варден пишет:

Аполлоний виртуозно владеет геометрической алгеброй, но не менее виртуозно умеет скрывать свой первоначальный ход мыслей. Из-за этого-то его книгу и трудно понимать; рассуждения его элегантны и кристально ясны, но что его привело именно к таким рассуждениям, а не к иным каким-нибудь,— об этом можно лишь догадываться.

До открытий Кеплера и Ньютона теория Аполлония практически применялась в основном для решения кубических уравнений, а также в оптике зеркал. Когда обнаружилось, что орбита материальной частицы в задаче двух тел есть одно из конических сечений, интерес к данным кривым резко возрос, и труды Аполлония были продолжены на новом математическом уровне.

Менделеев Дмитрий Иванович

27 января (8 февраля) 1834 г. – 20 января (2 февраля) 1907 г.

Биография

Русский химик Дмитрий Иванович Менделеев родился в Тобольске в семье директора гимназии. Во время обучения в гимназии Менделеев имел весьма посредственные оценки, особенно по латинскому языку. В 1850 г. он поступил на отделение естественных наук физико-математического факультета Главного педагогического института в Петербурге. Среди профессоров института были тогда такие выдающиеся учёные, как физик Э. Х. Ленц, химик А. А. Воскресенский, математик Н. В. Остроградский. В 1855 г. Менделеев окончил институт с золотой медалью и был назначен старшим учителем гимназии в Симферополь, но из-за начавшейся Крымской войны перевёлся в Одессу, где работал учителем в Ришельевском лицее.

В 1856 г. Менделеев защитил в Петербургском университете магистерскую диссертацию, в 1857 г. был утверждён приват-доцентом этого университета и читал там курс органической химии. В 1859-1861 гг. Менделеев находился в научной командировке в Германии, где работал в лаборатории Р. Бунзена и Г. Кирхгофа в Гейдельбергском университете. К этому периоду относится одно из важных открытий Менделеева – определение «температуры абсолютного кипения жидкостей», известной ныне под названием критической температуры. В 1860 г. Менделеев вместе с другими русскими химиками принимал участие в работе Международного конгресса химиков в Карлсруэ, на котором С. Канниццаро выступил со своей интерпретацией молекулярной теории А. Авогадро. Это выступление и дискуссия по поводу разграничения понятий атома, молекулы и эквивалента послужили важной предпосылкой к открытию периодического закона.

Вернувшись в Россию в 1861 г., Менделеев продолжил чтение лекций в Петербургском университете. В 1861 г. он опубликовал учебник «Органическая химия», удостоенный Петербургской АН Демидовской премии. В 1864 г. Менделеев был избран профессором химии Петербургского технологического института. В 1865 г. он защитил докторскую диссертацию «О соединении спирта с водой» (тема диссертации часто используется для обоснования легенды об изобретении им 40-градусной водки). В том же году Менделеев был утверждён профессором технической химии Петербургского университета, а через два года возглавил кафедру неорганической химии.

Приступив к чтению курса неорганической химии в Петербургском университете, Менделеев, не найдя ни одного пособия, которое мог бы рекомендовать студентам, начал писать свой классический труд «Основы химии». В предисловии ко второму выпуску первой части учебника, вышедшему в 1869 г., Менделеев привёл таблицу элементов под названием «Опыт системы элементов, основанной на их атомном весе и химическом сходстве», а в марте 1869 г. на заседании Русского химического общества Н. А. Меншуткин доложил от имени Менделеева его периодическую систему элементов. Периодический закон явился фундаментом, на котором Менделеев создал свой учебник. При жизни Менделеева «Основы химии» издавались в России 8 раз, ещё пять изданий вышли в переводах на английский, немецкий и французский языки.

В течение последующих двух лет Менделеев внёс в первоначальный вариант периодической системы ряд исправлений и уточнений, и в 1871 г. опубликовал две классические статьи – «Естественная система элементов и применение ее к указанию свойств некоторых элементов» (на русском языке) и «Периодическая законность химических элементов» (на немецком языке в «Анналах» Ю. Либиха). На основе своей системы Менделеев исправил атомные веса некоторых известных элементов, а также сделал предположение о существовании неизвестных элементов и отважился предсказать свойства некоторых из них. На первых порах сама система, внесённые исправления и прогнозы Менделеева были встречены научным сообществом весьма сдержанно. Однако после того, как предсказанные Менделеевым «экаалюминий» (галлий), «экабор» (скандий) и «экасилиций» (германий) были открыты соответственно в 1875, 1879 и 1886 гг., периодический закон стал получать признание.

Сделанные в конце XIX – начале XX вв. открытия инертных газов и радиоактивных элементов не поколебали периодического закона, но лишь укрепили его. Открытие изотопов объяснило некоторые нарушения последовательности расположения элементов в порядке возрастания их атомных весов (т.н. «аномалии»). Создание теории строения атома окончательно подтвердило правильность расположения Менделеевым элементов и позволило разрешить все сомнения о месте лантаноидов в периодической системе.

Учение о периодичности Менделеев развивал до конца жизни. Среди других научных работ Менделеева можно отметить цикл работ по изучению растворов и разработку гидратной теории растворов (1865–1887 гг.). В 1872 г. он начал изучение упругости газов, результатом которого стало предложенное в 1874 г. обобщённое уравнение состояния идеального газа (уравнение Клайперона – Менделеева). В 1880–1885 гг. Менделеев занимался проблемами переработки нефти, предложил принцип её дробной перегонки. В 1888 г. он высказал идею подземной газификации углей, а в 1891–1892 гг. разработал технологию изготовления нового типа бездымного пороха.

В 1890 г. Менделеев был вынужден покинуть Петербургский университет вследствие противоречий с министром Народного просвещения. В 1892 г. был назначен хранителем Депо образцовых мер и весов (которое в 1893 г. по его инициативе было преобразовано в Главную палату мер и весов). При участии и под руководством Менделеева в палате были возобновлены прототипы фунта и аршина, произведено сравнение русских эталонов мер с английскими и метрическими (1893–1898 гг.). Менделеев считал необходимым введение в России метрической системы мер, которая по его настоянию в 1899 г. была допущена факультативно.

Менделеев был одним из основателей Русского химического общества (1868 г.) и неоднократно избирался его президентом. В 1876 г. Менделеев стал членом-корреспондентом Петербургской АН, но кандидатура Менделеева в академики была в 1880 г. отвергнута. Забаллотирование Менделеева Петербургской АН вызвало резкий протест общественности в России.

Д. И. Менделеев был членом более 90 академий наук, научных обществ, университетов разных стран. Имя Менделеева носит химический элемент № 101 (менделевий), подводный горный хребет и кратер на обратной стороне Луны, ряд учебных заведений и научных институтов. В 1962 г. АН СССР учредила премию и Золотую медаль им. Менделеева за лучшие работы по химии и химической технологии, в 1964 г. имя Менделеева было занесено на доску почёта Бриджпортского университета в США наряду с именами Евклида, Архимеда, Н. Коперника, Г. Галилея, И. Ньютона, А. Лавуазье.